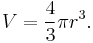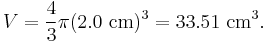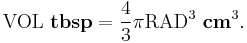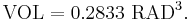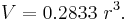Formula

In mathematics, a formula (plural: formulas or formulae [1]) is an entity constructed using the symbols and formation rules of a given logical language.

In science, a formula is a concise way of expressing information symbolically (as in a mathematical or chemical formula), or a general relationship between quantities. Colloquial use of the term in mathematics often refers to a similar construct.

Such formulas are the key to solving an equation with variables. For example, determining the volume of a sphere requires a significant amount of integral calculus; but, having done this once, mathematicians can produce a formula to describe the volume in terms of some other parameter (the radius for example). This particular formula is:

V =\frac{4}{3} \pi r^3.

Having obtained this result, and knowing the radius of the sphere in question, we can quickly and easily determine its volume. Note that the quantities V, the volume, and r the radius are expressed as single letters. This convention, while less important in a relatively simple formula, means that mathematicians can more quickly manipulate larger and more complex formulae.

Expressions are distinct from formulas in that they cannot contain an equals sign; whereas formulas are comparable to sentences, expressions are more like phrases.

In a general context, formulae are applied to provide a mathematical solution for real world problems. Some may be general: F = ma, which is one expression of Newton's second law, is applicable to a wide range of physical situations. Other formulae may be specially created to solve a particular problem; for example, using the equation of a sine curve to model the movement of the tides in a bay. In all cases however, formulae form the basis for all calculations.

Contents

In computing

In computing, a formula typically describes a calculation, such as addition, to be performed on one or more variables. A formula is often implicitly provided in the form of a computer instruction such as

Total fruit = number of Apples + number of Oranges.
Degrees Celsius = (5/9)*(Degrees Fahrenheit -32)

In computer spreadsheet terminology, a formula is usually a text string containing cell references, e.g.

=A1+A2

where both A1 and A2 describe "cells" (column A, row 1 or 2) within the spreadsheet. The result appears within the cell containing the formula itself (possibly A3, at end of values in column A). The = sign precedes the right hand side of the formula indicating the cell contains a formula rather than data. The left hand side of the formula is, by convention, omitted because the result is always stored in the cell itself and would be redundant.

Formulae with prescribed units

A physical quantity can be expressed as the product of a number and a physical unit. A formula expresses a relationship between physical quantities. A necessary condition for a formula to be valid is that all terms have the same dimension, meaning every term in the formula could be potentially converted to contain the identical unit (or product of identical units).

In the example above, for the volume of a sphere, we may wish to compute with r = 2.0 cm, which yields

V = \frac{4}{3}\pi(2.0 \mbox{ cm})^3 = 33.51 \mbox{ cm}^{3}.

There is vast educational training about retaining units in computations, and converting units to a desirable form, such as in units conversion by factor-label.

However, the vast majority of computations with measurements is done in computer programs with no facility for retaining a symbolic computation of the units. Only the numerical quantity is used in the computation. This requires that the universal formula be converted to a formula that is intended to be used only with prescribed units, meaning the numerical quantity is implicitly assumed to be multiplying a particular unit. The requirements about the prescribed units must be given to users of the input and the output of the formula.

For example suppose the formula is to require that 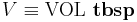V \equiv \mathrm{VOL}~\bold{tbsp}, where tbsp is the U.S. tablespoon (as seen in conversion of units) and VOL is the name for the number used by the computer. Similarly, the formula is to require 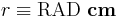r \equiv \mathrm{RAD}~\bold{cm}. The derivation of the formula proceeds as:

\mathrm{VOL}~\bold{tbsp} = \frac{4}{3} \pi \mathrm{RAD}^3~ \bold{cm}^3.

Given that 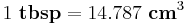1~\bold{tbsp} = 14.787~\bold{cm}^3 , the formula with prescribed units is

\mathrm{VOL} = 0.2833~\mathrm{RAD}^3.

The formula is not complete without words such as: "VOL is volume in tbsp and RAD is radius in cm". Other possible words are "VOL is the ratio of 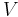V to tbsp and RAD is the ratio of r to cm."

The formula with prescribed units could also appear with simple symbols, perhaps even the identical symbols as in the original dimensional formula:

V = 0.2833~r^3.

and the accompanying words could be: "where V is volume (tbsp) and r is radius (cm)".

If the physical formula is not dimensionally homogeneous, and therefore erroneous, the falsehood becomes apparent in the impossibility to derive a formula with prescribed units. It would not be possible to derive a formula consisting only of numbers and dimensionless ratios.

References

  1. ↑ http://dictionary.reference.com/browse/formulae

See also